Splattalk

SplatTalk: 3D VQA with Gaussian Splatting

Abstract

• Language-guided 3D scene understanding
• 3DGS token to LLM
• zero-shot 3D VQA with only posed images

 

 

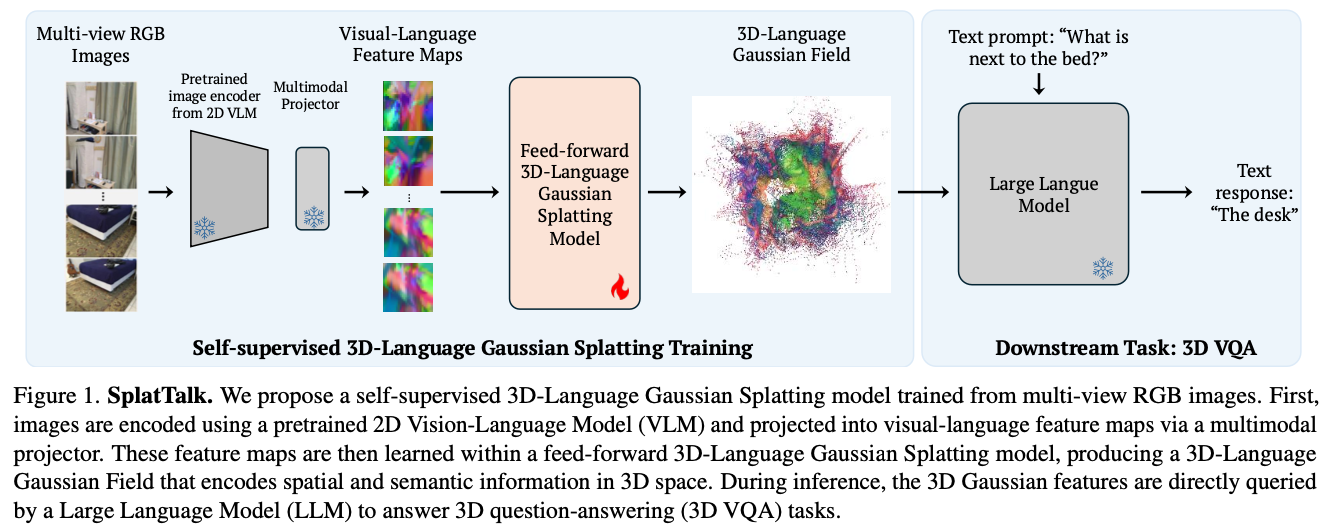
Motivation

• 2D VQA는 잘하는데 3D VQA는 잘 못함.
  • 3D VQA annotation이 비싸기 때문이다.
• 3D VQA는 2D 기반으로 풀면 안된다는 아이디어
  • segmentation + image encoder로 풀 경우 3D location, 3D holistic understanding 질문 답변 못함
• SplatTalk 제안
  • posed 2D RGB images 활용
  • 3DGS 만들고 3D token 추출하여 LLM input으로 direct하게 사용 <-> ChatSplat¹

 

 

Method

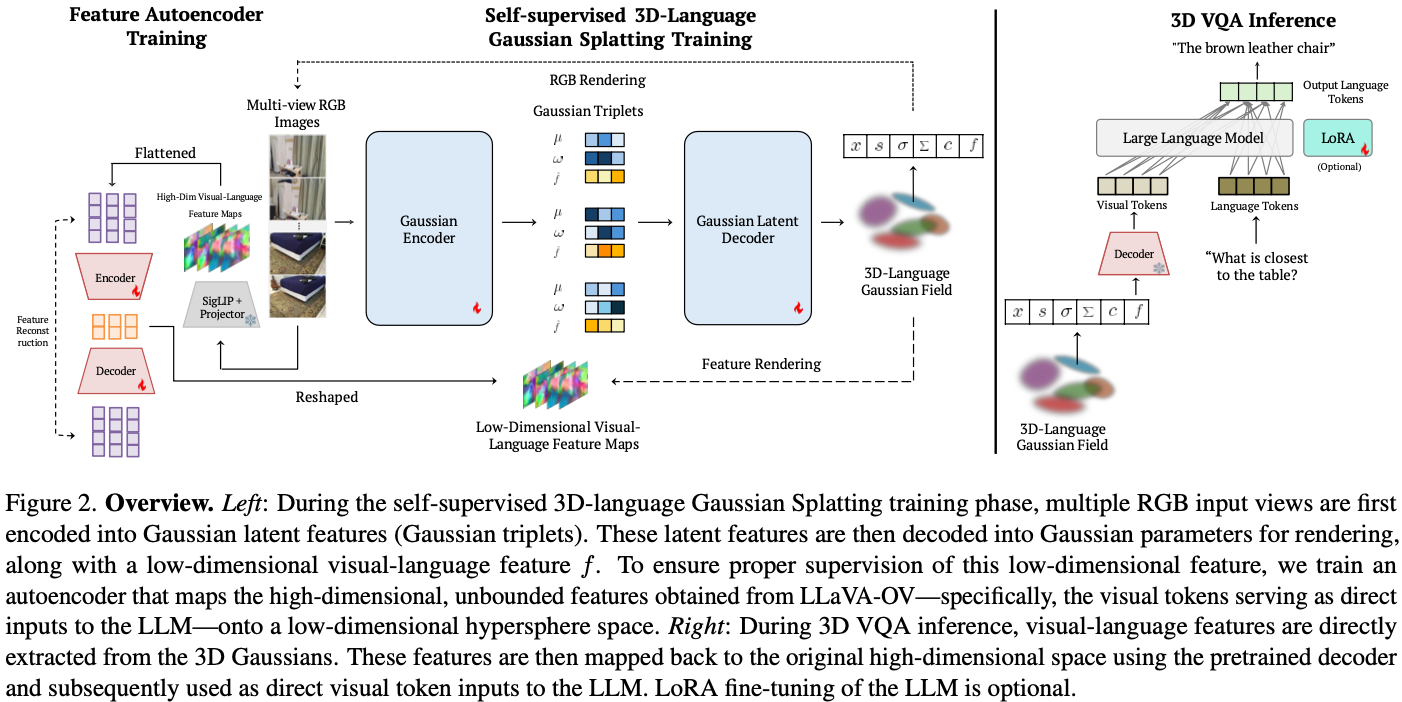
architecture는 다음과 같이 동작한다 (Fig. 2 참조).

• 각각의 RGB image는 Gaussian triplet으로 encode + low-dim encoder로 low-dim feature $f_{pseudogt}$를 얻는다.
• 다시 decode해서 3d Gaussian field + $f$를 만든다.
• 이 $f$를 $f_{pseudogt}$로 train한다.

이때 $f$는 LLM input으로 바로 활용되는 language aligned 3d feature이다.

flow는 다음과 같다:

1. Training the feature autoencoder
2. Self-supervised 3D-Language Gaussian Splatting Training
3. 3D VQA Inference

Integrating Language Features

• Visual Tokens for 2D Pseudo Groundtruth Features
  • 그냥 multimodal encoder 없이 image encoding하고 3DGS training하려면 projector retraining이 필요했다.
  • 이는 아마도 image가 high-dimension이라 input variation에 sensitive해지는 것으로 파악
• Feature Dimensionality Reduction
  • LLaVA의 feature dim은 3,584인데 이걸 256으로 reduction^{2 3 4}함.
• Joint-training RGB and Language
  • previous work와 다르게 RGB Gaussian과 language feature module을 joint-training했다.
  • 그렇게 했을 경우 holisitc한 scene information understanding에 그침.
  • 따라서 Gaussian 쪽에 decoder head를 또 붙여서 semantic feature for each 3D Gaussian을 capture

 

Extracting 3d Language Features

• inference할 때에는 3D Gaussian의 mean position에서 language feature를 extract한다.
  • the semantic feature $f$ derived from each Gaussian’s mean effectively captures the scene’s semantics
  • 그래서 f에 대한 expectation을 구해서 f에 대해 L2 loss를 minimize한다.

$$\mathcal{L} = \sum_{t,x} \left| \frac{ \sum_i \alpha_i f_i \mathcal{N}(x; \mu_i, \Sigma_i) }{ \sum_j \alpha_j \mathcal{N}(x; \mu_j, \Sigma_j) } - \mathbf{F}^{\text{gt}}_t(x) \right|^2$$

$$\nabla_{f_i} \mathcal{L} = 0 \iff f_i^* = \frac{ \sum_{t,x} R_i(t, x) \mathbf{F}^{\text{gt}}_t (x) }{ \sum_{t,x} R_i(t, x) }$$

• 이 식의 의미는 optimal 3D Gaussian feature $f^*$이 weighted sum of 2D feature map이 되는 것이다.
• segmentation literature에서는 Gaussian center에 대해서만 query하는 경우가 있다.
  • 이는 segmentation에서는 each Gaussian이 distinct하기 때문이다.
  • 그러나 3D reasoning에서는 individual Gaussian이 explicit object category를 encode하지 않을 수도 있기 때문에 위와 같은 방식으로 feature를 구한다.

 

 

Experiments

이쪽 domain의 performance metric을 잘 몰라서 패스

paper 참조하길 바란다.

 

 

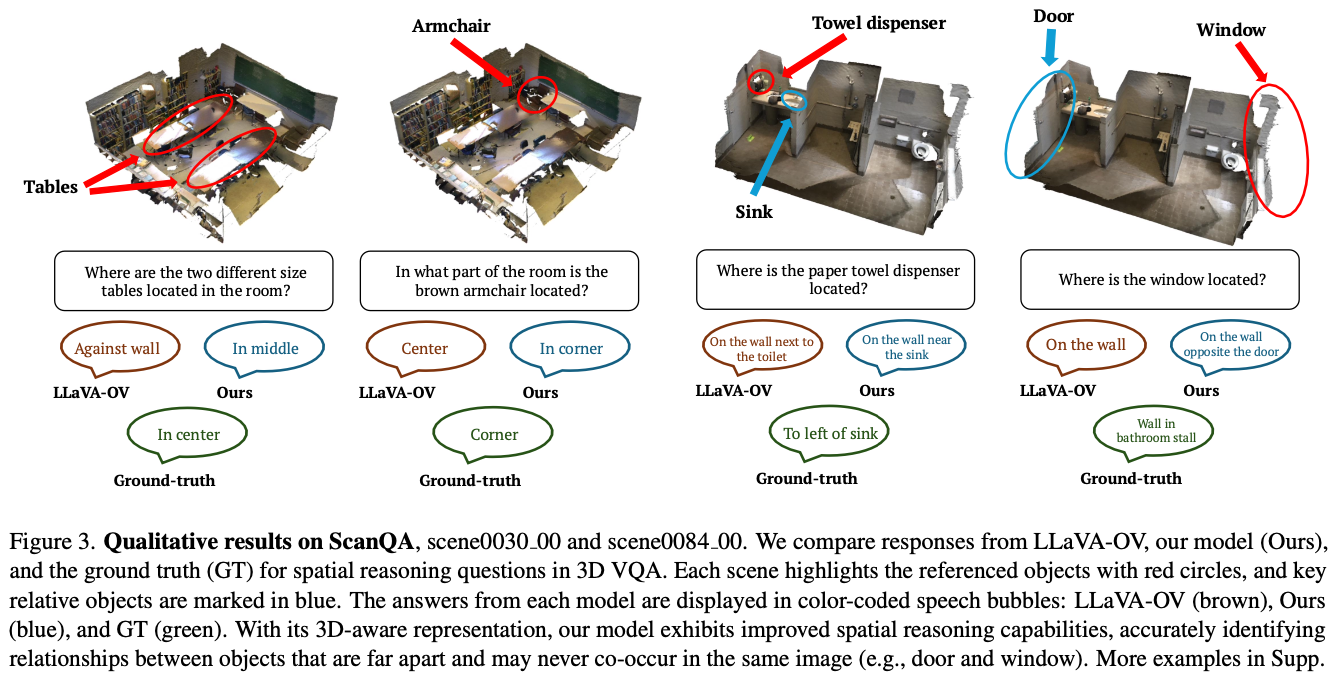
Discussion

• 3D gaussian에 대해 language aligned encoder가 없어서 이렇게 하는 것 같다.
• 재밌는 방식이긴 한데 방법이 decent해보이지는 않는다.

 

 

References