Asymtotic Notations
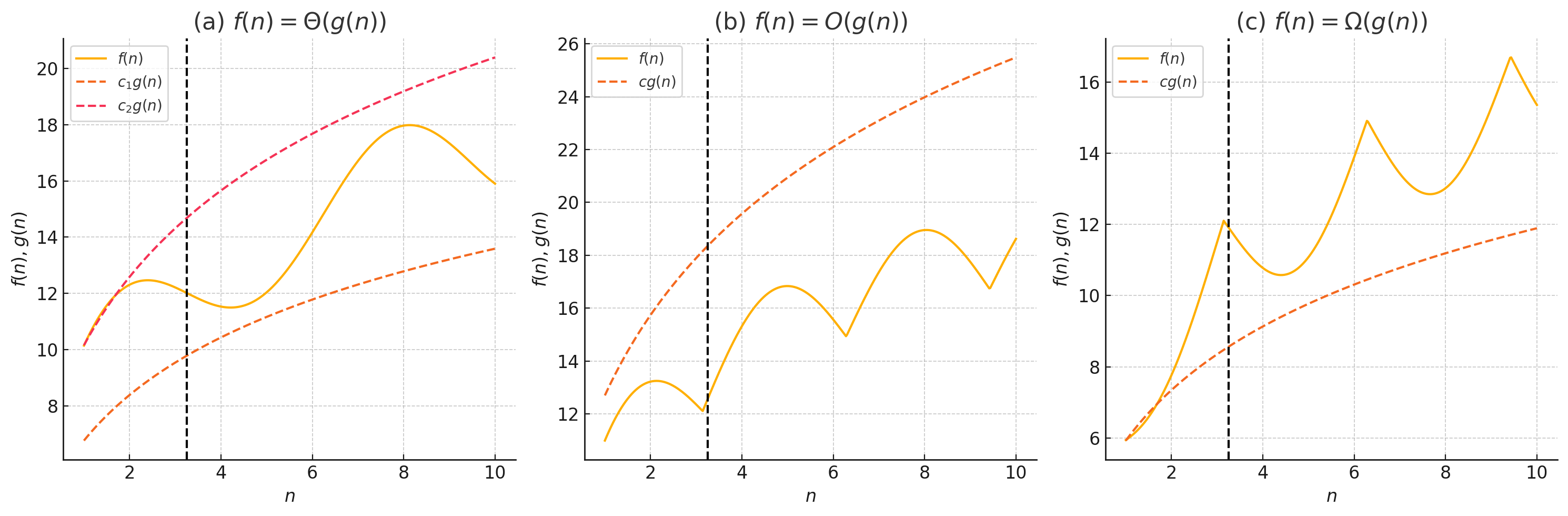
Θ-notation
$Θ(g(n))=\{f(n):\text{ there exist positive constants }c_1, c_2,\text{ and } n_0 \text{ such that } 0\le c_1g(n)\le f(n)\le c_2g(n)\text{ for all } n\ge n_0\}.$
- 즉 function $f(x)$이 grow할 때 $g(n)$로 upper bound & lower bound되는 경우 $g(n)$은 $f(n)$에 대한 asymtotically tight bound라고 하고 $f(n) \in Θ(g(n))$으로 쓴다.
- 본래 $Θ(g(n))$은 set이라 $f(n) \in Θ(g(n))$로 써야 하지만, abuse of notation으로 $f(n) = Θ(g(n))$로 쓰기도 한다.
$O$-notation
$O(g(n))=\{f(n):\text{ there exist positive constants }c\text{ and } n_0\text{ such that } 0\le f(n)\le cg(n)\text{ for all } n\ge n_0\}.$
- asymptotic upper bound만 존재하는 경우를 의미한다.
- 일반적으로 big-O notation은 asymtotically tight bound의 의미로 사용되기도 한다.
$Ω$-notation
$Ω(g(n))=\{f(n):\text{ there exist positive constants }c\text{ and } n_0 \text{ such that } 0\le cg(n)\le f(n)\text{ for all } n\ge n_0\}.$
- asymtotic lower bound만 존재하는 경우를 의미한다.
Theorems
Theorem 3.1
For any two functions $f(n)$ and $g(n)$, we have $f(n)=Θ(g(n))$$ if and only if $f(n)=O(g(n))$ and $f(n)=Ω(g(n))$. $\blacksquare$
→ trivial하므로 증명하지 않는다.
The Master Theorem
$$T(n)=aT(n/b)+f(n)$$where $a\ge1$ and $b>1$ are constants and $f(n)$ is an asymtotically positive function일 때, recursive algorithm의 time complexity를 빠르게 계산하는 방법이다.
- 여기서는 size $n$인 problem을 $a$개의 $n/b$ 크기의 subproblem으로 divide한 경우를 상정한다.
Theorem 4.1 (Master Theorem)
Let $a\ge1$ and $b>1$ be constants, let $f(n)$ be a function, and let $T(n)$ be defined on the nonnegative integers by the recurrence
$$T(n)=aT(n/b)+f(n)$$where we interpret $n/b$ to mean either $\lfloor n/b\rfloor$ or $\lceil n/b \rceil$. Then $T(n)$ has the following asymtotic bounds:
- If $f(n) = O(n^{\log_b a - \epsilon})$ for some constant $ε>0$, then $T(n) = \Theta(n^{\log_b a})$.
- If $f(n) = \Theta(n^{\log_b a})$, then $T(n) = \Theta(n^{\log_b a} \log n)$
- If $f(n) = \Omega(n^{\log_b a + \epsilon})$, for some constant $ε>0$, and if $af(n/b)\le cf(n)$ for some constant $c<1$ and all sufficiently large $n$, then $T(n) = \Theta(f(n))$. $\blacksquare$
- 주요 아이디어는 두 term 중 어떤 것이 solution을 푸는 시간에 domiant한지 구분하는 것이다.
- 1번의 경우 $f(n)$이 $aT(n/b)$보다 작은 term에 upper bound되므로 전체 time은 왼쪽 term에 대해서만 asymptotically tight bound된다.
- 2번의 경우 두 term의 크기가 같다. 따라서 $\log n$번 recursion되는 factor를 곱한 $\Theta(n^{\log_b a} \log n)$에 tightly bound된다.
- 3번의 경우 $f(n)$ term의 time이 더 크므로 $f(n)$에 대해서만 tightly bound된다.
- 다만 실제로 $a$ factor에 의해 dominancy가 달라질 수 있으므로 regular condition $af(n/b)\le cf(n)$을 satisfy하는지 확인하여야 한다.
- example
- 예컨대 merge-sort에서는 다음과 같이 time complexity가 계산된다.
- $T(n)=2T(n/2)+O(n)$
- $f(n)=n$이므로 $Θ(n)$에 asymptotically tight bound된다.
- 좌측 term인 $Θ(n^{\log_2 2})$와 같으므로 case 2이다.
- 따라서 전체 time은 $T(n)=Θ(n\log n)$으로 계산된다.
- proof는 생략한다.
Refereces
T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms, 3rd Edition. MIT Press, 2009.